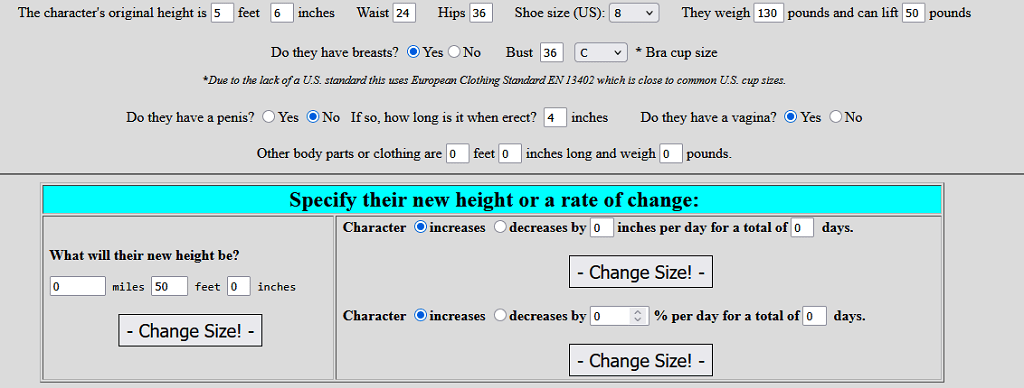
You wake up in the dead of night. Your forehead is beading with sweat. An unyielding question keeps churning within your brain keeping you from getting some much-needed sleep.
“If a 5’6″ tall woman grew to 50′ tall then how wide would her hips be in feet and inches?“
We’ve all been there before, but how do we find relief? For years there was no satisfactory response, only wildly inaccurate conjecture. But no longer! Now we can learn the answer with the handy dandy Sizechange Calculator, version 0.7 😎 (Click here to access the calculator hosted at Giantess City.)
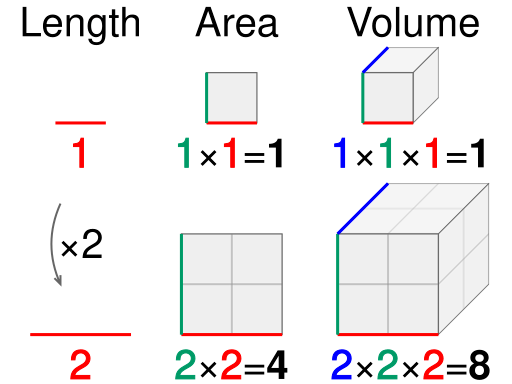
This calculator computes data using the square-cube law. Humans are three dimensional beings and this calculator assumes that a human will change equally in all three of those dimensions. If their height increases in size by a factor of 2 then their other two dimensions will also increase in size by a factor of 2. So, a man who is twice as tall as when he started ergo if he increased in size by a factor of 2 then he will weigh eight times as much (since weight is a measure of mass which is determined by volume). This is because his volume is that factor cubed, 2 x 2 x 2. (Click here to learn more about the square-cube law.)
The Sizechange Calculator can handle three main functions:
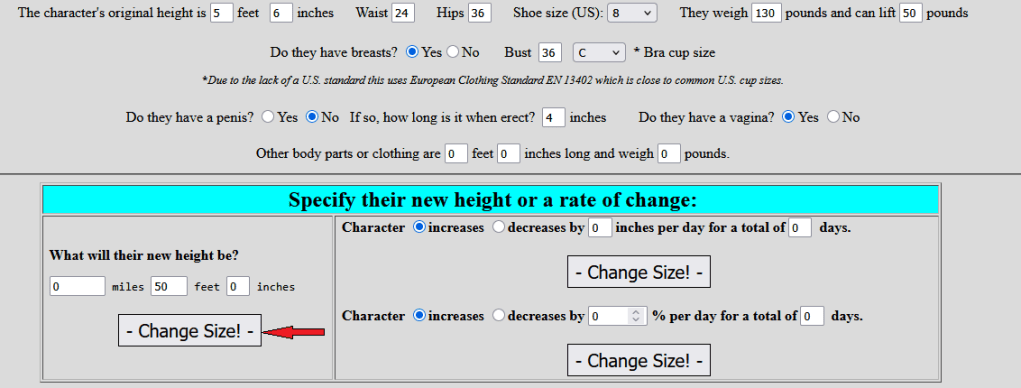
Function #1 ~ Designated Size
The first function computes the size of a character after they reach a specified height, either smaller or larger than their starting measurement. Assuming even and proportional increase it answers questions like how much a 5’6″ 130lb woman would weigh if she became 50′ tall. By the way the answer is she would weigh 48 tons 1,670 pounds, using only pounds that converts to 97,670lb. (That figure uses short tons where each one is equivalent to 2,000 pounds.)
** WARNING MATH **
For those interested in the math we can compute how much a 5 foot 6 inch tall woman who initially weighs 130lb will weigh after she becomes 50 foot tall by first finding the factor of her height increase. Five foot six inches equals 66 inches tall while fifty feet equals 600 inches tall. The height increase from 66 to 600 inches can be factored by dividing the new height, 600 inches, by the starting height, 66 inches. Doing that math gives us an answer of 9.090909090909091. So, the woman increased in height by a factor of 9.090909090909091. Her volume then increased by that factor cubed, 9.090909090909091 x 9.090909090909091 x 9.090909090909091 which equals 751.3148009015778. Then you take her weight at 5’6″ which was 130lb and times that number, 130, by the size factor cubed, 751.3148009015778, and you get 97,670.92411720511, rounding down to the nearest whole number gives us 97,670lb. TL;DR Growing things get heavy really fast!

Other measurements include how wide are her hips (10‘5″), how high are her knees (13‘4.7″), how wide are her shoulders (13’9″), how large is her bust (27’3″, assuming she started at a 36C), etc. Of note, those standard (or imperial) measurements are also converted to metric on the right side of the form.
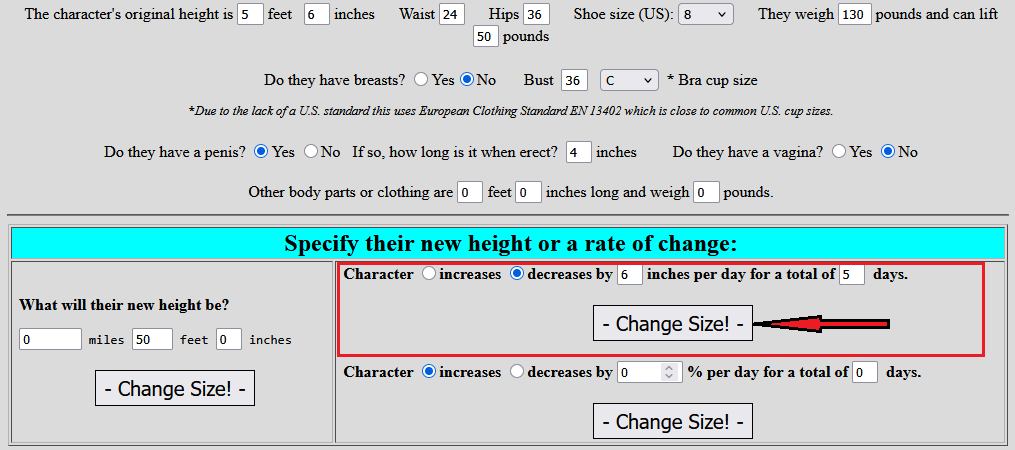
Function #2 ~ Change over Time by a Set Amount
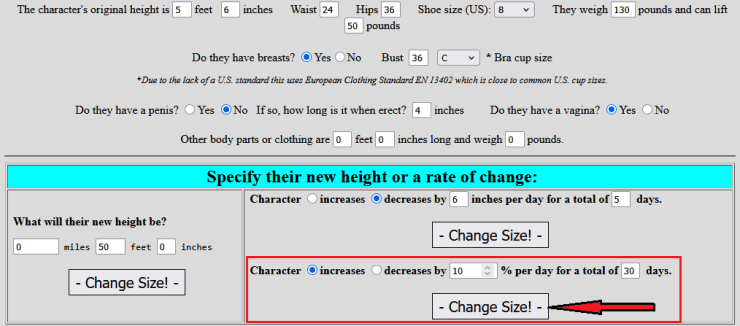
Computing the size of a character after a set amount of days in which they decrease or increase in size by a number of specified inches. This answers questions like “How high above ground are a 5’6″ man’s knees after he has lost 6 inches of height per day for a period of 5 days?” The answer is his knees would be 9.6″ off the ground after five days of shrinking by that consistent amount.
Other measurements include his weight (21lb), how wide are his shoulders (9″), etc. Of course those United States customary units are also converted to metric on the right side of the form.
Function #3 ~ Change over Time by a Set Percentage
Computing the size of a character after they increase or decrease in size by a set percentage each day. Answering questions like how large would a 5’6″ woman’s 36C breasts be after she increased in height by 10% per day for a period of thirty days. Answer is she would have a 52’6″ bust. A slew of other measurements are also given in standard (ergo feet and inches) and metric (ergo meters and centimeters).
New Capability in Version 0.7
After I released Sizechange Calculator version 0.6 there were requests to add even more data points ranging from clothing, such as sock length, to body parts such as a person’s stomach and throat. So, I created a catch-all option entitled “Other body parts or clothing.”
Using this new option a person can enter initial data such as the length of a woman’s hair when she is normal size then compute hair length after she becomes 50 foot tall. If a 5’6″ woman had 1’1″ long hair then after she becomes 50″ tall her hair would be 9’10” long. Similarly, if that woman had 9″ long socks to begin with and they increased in size with her body then the woman’s socks would be 6’9.8″ long after her transformation.
Furthermore, if you create a scenario in which a woman’s clothes and other accouterments change in size with her then you can compute the weight of her sandals. If her sandals weighed 1lb when she was 5’6″ tall then they would weigh 751lb when she becomes 50′ tall. If her stomach was normally 6″ inches wide then it would become 4’6″ wide and if her throat was normally 4″ long then it would become 3′ long.
Limitations, a.k.a. the Party Pooper Section
The calculator provides consistent and “realistic” measurements for atypically small and unusually large human or humanoid characters. That computed data provides verisimilitude to stories so the end result is that they should feel more real. However, this does not mean that it is true that a 50 foot tall human would have these exact measurements. This calculator assumes that a human being’s proportional dimensions would not change. For example, it assumes that a 5’6″ tall woman will not have thicker legs, in relation to the rest of her body, when she becomes 50′ tall.

By contrast in the HBO series Game of Thrones, giants had thicker legs than humans to compensate for their greater weight. For example see the Game of Thrones giant Mag the Mighty, played by Neil Fingleton, standing next to a human.
Stanford University paleobiologist Jonathan Payne discussed the giant gorilla King Kong from “Kong: Skull Island” in a 2017 Smithsonian magazine article entitled “How Big Can a Land Animal Get?” Dr. Payne stated “King Kong as shown in the movie probably isn’t a physically viable organism.” He also said “As you get bigger you need to dedicate more and more of your body mass to your bones to support yourself.” In that same article University of New Mexico paleoecologist Felisa Smith agreed saying “Larger animals need bigger and thicker limbs to hold themselves up.“
Unfortunately, the human body is not made to scale. A 50-foot tall bikini model would be unable to function with skinny limbs. She would be so heavy as to be immobile and she would experience other problems with breathing, circulating blood, keeping her body warm, etc. Keeping her original proportions a 50-foot tall giantess would require steel-like bones and Superman-like muscles to support and move her body. Maybe she would also require multiple brains (like the kaiju in Pacific Rim) to control her body or weird organs (like the “frog” in horse hooves) to boost her circulatory system.
Even relatively minor deviations (well, minor compared to Nancy Archer) such as reaching heights over eight feet tall causes health complications putting stress on people’s bones, heart and circulatory systems, etc. It is rare for someone over eight feet tall to live to old age.
Furthermore, the Sizechange Calculator can not handle uneven growth. So, if a character does not proportionally increase in all dimensions then its results will be inaccurate. For example, if a character elongates (like the lady on the cover of Giantess Fan’s “Girls on the Grow” #4, pictured below) then the calculator will not work as intended.

Additionally, there is a known issue with the amount of force displayed under the “Movement” section. Force or energy is measured in joules in the lines which explain how many joules their hops, steps, and stomps produce.
The problem is that joules should be much higher after a character grows because this calculator assumes that the character moves at the same speed relative to the size of their body. So, if it takes a regular sized man a few seconds to walk one step forward the Sizechange Calculator assumes it will take him the exact same amount time to walk one step forward after he becomes a giant. However, in reality, because the distance increased it should take more time. So, by assuming that the giant can take a step in the same amount of time then their feet have to move faster in order to cover more distance in the same amount of time. More speed means more force. (NOTE: Thanks to Crovenard for pointing out this issue to me on Bluesky.) I hope to correct this issue in the next update, sometime in the future.
Giants and tinies are fantasy beings. It would take a lot more research to compute the dimensions for a scientifically accurate and fully plausible giant. The goal of the Sizechange Calculator is much more humble. I merely hope it will serve as a helpful tool to add a little more consistency and realism to fictional works.
If you have questions or concerns please comment below or send an e-mail to solomong_author@outlook.com
Until next time folks, keep growing!
This article was written by SolomonG and is protected under Fair Use copyright law.
All Rights Reserved.

Also they would also sink down into the ground, if they’re too heavy.
LikeLiked by 1 person